Algebraic independence

From Wikipedia, the free encyclopedia

In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K. This means that for every finite sequence α₁, ..., α_n of elements of S, no two the same, and every non-zero polynomial P(x₁, ..., x_n) with coefficients in K, we have

P(α₁,...,α_n) ≠ 0.

In particular, a one element set {α} is algebraically independent over K if and only if α is transcendental over K. In general, all the elements of an algebraically independent set over K are by necessity transcendental over K, but that is far from being a sufficient condition.

For example, the subset {√π, 2π+1} of the real numbers R is not algebraically independent over the rationals Q, since the non-zero polynomial

yields zero when √π is substituted for x₁ and 2π+1 is substituted for x₂.

The Lindemann-Weierstrass theorem can often be used to prove that some sets are algebraically independent over 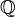. It states that whenever α₁,...,α_n are algebraic numbers that are linearly independent over Q, then e^α₁,...,e^α_n are algebraically independent over Q.

It is not known whether the set {π, e} is algebraically independent over Q. Nesterenko proved in 1996 that {π, e^π, Γ(1/4)} is algebraically independent over Q.

Given a field extension L/K, we can use Zorn's lemma to show that there always exists a maximal algebraically independent subset of L over K. Further, all the maximal algebraically independent subsets have the same cardinality, known as the transcendence degree of the extension.